\[\newcommand{\norm}[1]{\left\lVert#1\right\rVert}\]

In this project, we’ll explore multiple strategies for aligning multiple monochrome captures of an image into a single color image. There are 2 main strategies employed: naive search and image pyramid. For bells and whistles, an automatic edge cropper as well as a feature-based image metric were implemented.

Problem Statement.

We have 3 monochrome images captured independently and the task is to merge each into a single color image. Since these images were captured separately, they are not guaranteed to line up perfectly; so simply merging three $W\times H\times1$ numpy arrays into one $W\times H\times3$ array won’t work. Instead, we need to find a displacement for each color channel to ensure image details line up.

1. Naive Search (with gradient-based image metric)

The first obvious approach to try would by to search over a grid of possible displacements to find the best alignment. To measure the quality of each alignment, we use a simple metric function. Something such as $\norm{im_1 - im_2}_2$ would do. This works well for most images, except for a few such as emir.tif.

To make the L2 norm works for emir, I decided to take the norm on the gradients of an image, rather than directly on its color value. The approximated gradient in the x direction of an image could be computed as its convolution with the Prewitt operator: $\frac{dIm}{dx} = G_x * Im$ where $G_x$ is the Prewitt kernel and is defined as follows: $G_x = \begin{bmatrix}+1 & +1 & +1 \\ 0 & 0 & 0 \\ -1 & -1 & -1 \end{bmatrix}$ and $G_y = G_x^{T}$.

$\frac{dIm}{dy}$ is defined analogously.

The revised norm for images $Im_1$ and $Im_2$ is then $\sqrt{\norm{\frac{dIm_1}{dx} - \frac{dIm_2}{dx}}^2 + \norm{\frac{dIm_1}{dy} - \frac{dIm_2}{dy}}^2}$.

Since the edges of the monochrome images are highly irregular and don’t really reflect the quality of an alignment, I also excluded a margin around the edges before taking the norm. Using this new norm, we see a marked improvement for emir as well as other images.

L2 on color value	L2 on gradient

2. Image Pyramid.

The first approach works well if we aren’t constrained by time since doing a blind search for a large image (such as emir.tif) could be very time consuming. To have more a reasonable runtime, we will employ image pyramid.

The idea is to align the image at multiple scales, starting from the coarsest one. At the coarsest scale, we search over a large grid since it is faster to compute the norm for smaller images. As the resolution increases, we search over increasingly smaller grids to make finer adjustments to the original displacement.

Suppose at each level of the pyramid we downsize the image by a factor of 2x (with anti-aliasing enabled so skimage internally applies some Gaussian smoothing). Let $\Delta_i$ be the displacement at the $i$-th level in the pyramid and $G_i$ be the displacement at level $i$ found by searching over a grid. The displacement at level $i$ is then $\Delta_i = G_i + \Delta_{i-1} \times 2$.

This approach yields great improvements in runtime. For example, running emir.tif only took less than 10 seconds! Here are some results:

3. Auto-cropping

The images produced tend to have black edges or edges that were artifacts of the alignment process so we’d like to remove them. For vertical edges, I noticed that taking the gradient in the $x$ direction would result in really small gradients near the edges. Here’s an example of the gradient (in the x direction) of melons.tif (inverted for easier viewing).

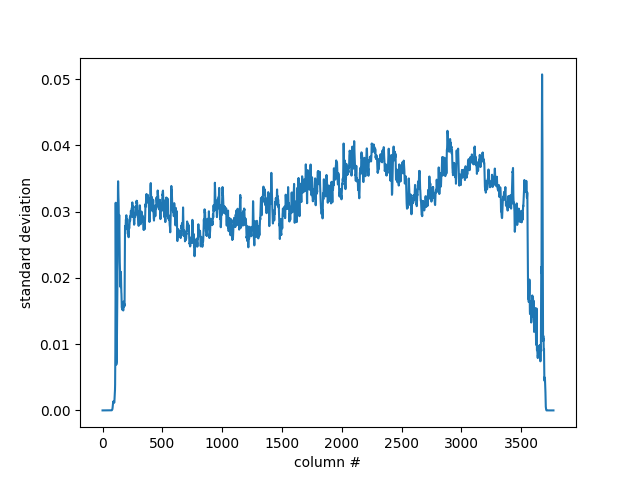
If we took the standard deviation of the pixel values of each column (so np.std(grayscale(im)[:, col])), we have the following graph. Notice the stark increase in the variance of the pixel values train

What remains is to crop the picture at these outlying columns. The first approach is to simply use the statistical definition for outliers (i.e. $mean + 1.5\times std$). This is fairly successful at cropping out the black edges. Here are some results.

Before	After

Appendix

Here are all the pictures (without autocrop) and their displacements

Picture	Red displacement	Green displacement
	(12, 3)	(5, 2)
	(58, -4)	(25, 4)
	(106, 42)	(49, 24)
	(123,13)	(60, 17)
	(89, 23)	(40, 17)
	(177, 13)	(80, 10)
	(3, 2)	(-3, 2)
	(108, 36)	(51, 27)
	(140, -27)	(33, -11)
	(175, 37)	(79, 30)
	(7, 3)	(3, 3)
	(86, 33)	(42, 8)

For three_generations.tif, I found that aligning both red and blue to green works better so here is the displacement:

Picture	Red displacement	Blue displacement
	(-53, -13)	(59, -5)

Similarly, for lady.tif, I found that aligning green and blue to red works better:

Picture	Blue displacement	Green displacement
	(-63, -4)	(-119, -13)